이 포스팅은 cs231n 강의와 활용된 자료를 바탕으로 한 포스팅입니다.
처음 공부하였을 때 정리한 포스팅이라 내용이 많이 부족합니다.

1. Recurrent Neural Networks
1.1 RNN : Process Sequence

RNN은 네트워크가 다양한 입력, 출력을 다룰 수 있게 해준다. 그리고 가변 길이의 데이터를 다루기 위해 필요한 일반적인 방법(paradigm)이다.
* one to many 모델 : 입력은 단일 입력이지만 출력은 가변 출력이다. (ex. Image Captioning / 이미지를 그를 설명하는 던어들을 만들어 낼 때)
* many to one 모델 : 입력은 가변 입력이며 출력은 단일 출력이다. (ex. Sentiment Classification / 입력은 문장이 될 수 있으며, 출력의 경우 문장의 '감정'을 분류한 값(긍정/부정)이다.)
* many to many 모델(1) : 입/출력 모두 가변이다.(ex. Machine Translation / 문장을 입력하고 문장을 출력받을 때)
* many to many 모델(2) : 입/출력 모두 가변이다.(ex. Video classification on frame level / 비디오가 입력이고 매 프레임마다 classificastion을 해야 하는 상황)
1.2 RNN을 활용한 예시

입/출력은 고정이지만 sequential processing인 경우에 RNN은 상당히 유용하다.

모델은 Train time에서 본 이미지들을 바탕으로 새로운 이미지를 생성해내는데, 이를 위해 RNN을 이용할 수 있다. 순차적으로 전체 출력의 일부분씩 생성해낸다. 이 경우에도 전체 출력은 고정된 길이지만, RNN을 이용해서 일부분씩 순차적으로 처리할 수 있다.
1.3 RNN의 기본 구조

RNN이 매 단계마다 값을 출력하는 단계 : ① RNN이 입력을 받는다 → ② 'hidden state'를 업데이트한다. → ③ 출력 값을 내보낸다. ('hidden state'는 RNN 내부에 있으며 RNN이 새로운 입력을 불러들일 때마다 매번 업데이트가 된다.)
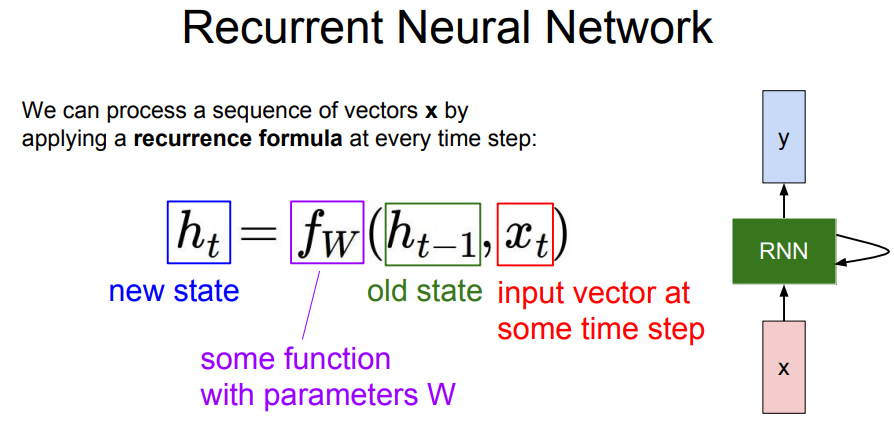
RNN은 hidden state를 반복적으로 거치며, '함수 f'로 '재귀적인 관계'를 연산할 수 있도록 설계된다. 이 때 함수 f와 사용되는 가중치 W는 매 스텝 동일하다.
함수 f는 '이전 상태의 hidden state(h_t-1)'와 '현재 상태의 입력(x_t)'을 입력으로 받는다. 그리고 '다음 상태의 hidden state(h_t)'를 출력한다. 그리고 다음 단계에서는 h_t와 x_t+1이 입력이 된다.
RNN에서 출력값(y)를 가지려면 h_t를 입력으로 하는 FC-Layer를 추가해야 한다. FC-Layer는 매번 업데이트되는 hidden state(h_t)를 기반으로 출력 값을 결정한다.

수식적으로 간단하게 표현해보면 다음과 같다. 우선, 두 입력(h, x)가 있다.
가중치 행렬(W_xh)와 입력(x_t)의 곱으로 나타낼 수 있다. 또한 가중치 행렬(W_hh)는 이전 hidden state(h_t-1)와 곱해진다. 곱한 값들을 더해주고 시스템에 비선형을 구현하기 위해 tanh를 적용한다.
매 스텝마다 출력 y를 얻으려면 hidden state(h_t)를 새로운 가중치 행렬(W_hy)와 곱해준다. 매 스텝에 출력 y는 class score가 될 수 있다.

1) RNN이 hidden state를 가지며 이를 '재귀적으로' feed back 한다.
첫 step에 있는 initial hidden state(h_0)는 0으로 초기화를 시킨다. 그리고 입력 x_t가 있다. h_0과 x_1이 f_w의 입력으로 들어가게 된다. f_w(h_0, x_1)의 출력은 h_1이 된다. 이 과정을 계속 반복한다.
여기서 중요한 것은 '동일한 가중치 행렬 W가 매번 사용된다는 점'이다. (매번 h, x는 달라지지만 W는 매번 동일하다) 이 RRNN 모델의 backpropagation을 위한 W의 gradient를 구하려면 각 스텝에서의 W에 대한 gradient를 전부 계산한 뒤에 값들을 모두 더해주면 된다.

RNN 출력 값인 h_t가 또 다른 네트워크의 입력으로 들어가서 y_t를 만들어낸다. y_t는 매 스텝의 class score가 될 수 있다. 그리고 y_t에 대한 Loss를 계산할 수 있으며 이들의 합이 최종 Loss이다.

감성분석(sentiment classification)과 같은 경우에는 네트워크의 최종 hidden state에서만 결과 값이 나온다. 최종 hidden state가 전체 시퀀스의 내용에 대한 일종의 요약으로 볼 수 있기 때문이다.

고정 입력(x)은 모델의 initial hidden state를 초기화하는 용도로 사용한다. 그리고 RNN은 모든 스텝에서 출력 값을 가진다.

sequence to sequence 모델은 machine translation에 사용하는 모델이다. 이것은 many to one과 one to may 모델을 합친 것으로 볼 수 있다. 2개의 stage로 구성되는데, encoder와 decoder 구조이다. encoder는 many to one을 수행하고 decoder은 one to many를 수행한다. encoder는 가변 입력을 받는다. (ex. English sentence) encoder의 최종 hidden state를 통해 전체 sentence를 요약한다. decoder의 입력은 요약된 하나의 벡터이며, 출력은 sentence(ex. France sentence)가 된다.
1.4 Character-level Language Model

네트워크는 문자열 시퀀스를 읽고 현재 문맥에서 다음 문자를 예측해야한다.
Train time에서는 각 단어들을 입력으로 넣어줘야 한다. 여기서 y_t는 어떤 문자가 'h' 다음에 올 것 같은지를 예측하는 값이다. hidden state를 이용해서 적절한 값을 예측해야 한다.
이 과정을 반복하여 다양한 문장으로 모델을 학습시킨다면 모델은 이전 문장의 문맥을 참고해 다음 문자가 무엇일지를 학습해야 한다.

Test time에서는 어떨까?
학습시킨 모델을 활용할 수 있는 방법 중 하나는 모델로부터 Sampling을 하는 것이다. Train time에 모델이 봤을 법한 문장을 모델 스스로 생성해내는 것이다.
h를 입력하면 모든 문자에 대한 스코어를 얻을 수 있는데, 이 스코어를 다음 글자를 선택할 때 이용한다. 스코어를 확률분포로 표현하기 위해 softmax함수를 사용할 수 있다.
Q. 가장 높은 스코어를 선택하면 되는데, 왜 굳이 확률분포에서 샘플링을 하는가?
이 예제의 경우, 가장 스코어가 높은 값만 사용하면 올바른 결과를 낼 수 없었기에 확률분포에서 샘플링하면 알맞은 문장을 잘 생성할 수 있다. 확률분포에서 샘플링 또는 가장 높은 값 선택하는 것을 모두 사용할 수 있는데 샘플링하는 방법을 사용하면 일반적으로는 모델에서의 다양성을 얻을 수 있다.
Q. Test time에 softmax vector를 one hot vector 대신에 넣어줄 수 있는가?
2가지 문제가 발생하게 된다.
첫번째, 입력이 Train time에서 보았던 입력과 달라진다.
두번째, 실제로는 vocabularies가 아주 크다. 실제로는 one hot vector를 dense vector(밀집 벡터)가 아닌 sparse vector operation으로 처리한다. 만약 softmax vector를 연산해야 한다면 연산량이 엄청 클 것이다.
그렇기에 Test time에서도 one hot을 사용하는 이유이다.

시퀀스 별 출력값들의 Loss를 계산해 final loss를 얻는데, 이를 'backpropagation through time'이라고 한다. forward pass의 경우에는 전체 시퀀스가 끝날 때까지 출력값이 생성된다. 반대로 backward pass에서도 전체 시퀀스로 Loss를 계산해야 한다. 하지만 시퀀스가 아주 긴 경우에는 문제가 될 수 있다. gradient를 계산하려면 전체를 거쳐야 하므로 학습이 매우 느릴 것이며 메모리 사용량도 많을 것이다.

실제로는 'truncated backpropagation'을 사용한다.
Train time에 한 스텝을 일정단위로 자른후 그만큼 forward pass를 하고 서브 시퀀스의 loss를 계산한다. 그리고 gradient step을 진행한다.

이 과정을 반복하지만 이전 batch에서 계산한 hidden states는 계속 유지한다. 다음 batch의 forward pass를 사용할 때 이전의 hidden state를 이용한다. 그리고 gradient step은 현재 batch에서만 진행한다.
2. Image Captioning

Image Captioning 모델은 입력은 이미지, 출력은 자연어로 된 Caption이다. Caption은 가변길이로 Caption마다 다양한 시퀀스 길이를 가지고 있다.

입력 이미지를 받기 위한 CNN 모델이 있다. CNN은 요약된 이미지 정보가 들어있는 Vector를 출력한다. 이 Vector는 RNN의 초기 Step의 입력으로 들어간다. 그러면 RNN은 Caption에 사용할 문자들을 만든다.

이전까지의 모델에서는 RNN 모델이 두 개의 가중치 행렬인 '현재 스텝의 입력, 이전 스텝의 hidden state'을 입력으로 받았다. 그리고 이것을 조합하여 다음 hidden state를 얻었다.
하지만 이제는 이미지 정보도 추가로 더해줘야 한다. 가장 쉬운 방법은 세번째 가중치 행렬을 추가하는 것이다. 그러면 다음 hidden state를 계산할 때마다 모든 스텝에 이미지 정보를 추가한다.

vocabulary의 모든 스코어에 대한 분포를 계산해야 한다. 그 분포에서 샘플링을 하고 단어를 다음 스텝의 입력으로 넣어준다. 이를 반복하고 모든 스텝이 종료되면 한 문장이 만들어진다.

이 모델을 학습한 후의 결과이다.

하지만 Train time에서 보지 못한 데이터에 대해서는 잘 작동하지 않는 것을 확인할 수 있다.
2.1 Attention 모델

이 모델은 Caption을 생성할 때 이미지의 다양한 부분을 집중해서 볼 수 있다.

Forward pass 시에 매 스텝 vocabulary에서 샘플링을 할 때, 모델이 이미지에서 보고싶은 위치에 대한 분포를 만들어낸다. 이미지의 각 위치에 대한 분포는 Train time에 모델이 어느 위치를 봐야하는지에 대한 attention이라고 할 수 있다.
첫번째, hidden state(h0)는 이미지의 위치에 대한 분포를 계산한다. 이 분포(a1)를 다시 벡터 집합(LxD Feature)과 연산하여 이미지 attention(z1)을 생성한다.

하나의 vocabulary의 각 단어들의 분포(d1), 이미지 위치에 대한 분포(a2)가 출력된다. 이 과정을 반복하면 매 스텝마다 값 2개의 (a, d)가 계속 만들어진다.

Train을 마치면, 모델이 caption을 생성하기 위해서 이미지의 attention을 이동시키는 모습을 볼 수 있다.
soft attention은 모든 특징과 모든 이미지 위치 간의 weighted combination을 취하는 경우다. 반면 hard attention은 모델이 각 타임 스텝마다 단 한 곳만 보도록 강제한 경우다. 한 곳만 보는 것에 어려움이 있기에 hard attention을 학습시키려면 기본 backpropagation보다 좀 더 fanier한 방법을 써야한다.

Attention Model을 학습시키고 나서 Caption을 생성해보면 실제로 모델이 Caption을 생성할 때 의미 있는 부분에 attention을 집중한다는 것을 알 수 있다. 모델이 의미있는 영역에 집중하는 것이 올바른 일이라는 것을 스스로 알아내었다.
2.2 RNN + Attention

RNN + Attention 조합은 Image Captioning 뿐만 아니라 다양한 것들을 할 수 있다.
이미지와 질문을 입력하여 질문에 대한 답을 맞추는 것이다.

이 모델도 RNN과 CNN으로 만들 수 있다. RNN → CNN
모델이 정답을 결정하기 위해서는 이미지에 대한 attention을 만들어내는 것을 볼 수 있다.
3. Multilayer RNNs

지금까지는 단일 RNN 레이어를 사용해 hidden state가 하나뿐이었다. 하지만 우리가 자주 보게 될 모델들은 Multi-Layer RNN이다.
3-Layer RNN이 있다. 입력이 첫번째 RNN으로 들어가서 첫번째 hidden state를 만들어낸다. RNN 하나를 돌리면 hidden state 시퀀스가 생기고 이것을 다른 RNN의 입력으로 넣어줄 수 있다. 그러면 두번째 RNN layer가 만들어낸 또 다른 hidden states 시퀀스가 생긴다.
이렇게 하는 이유는 모델이 깊어질수록 다양한 문제들에서 성능이 좋아지기 때문이다.
4. Vanilla RNN Gradient Flow

Vanilla RNN은 입력으로 X_t와 이전 hidden state인 h_t-1을 쌓고 가중치 행렬 W와 행렬곱연산을 한 후 tanh를 씌워 다음 hidden state(h_t)를 만든다.
backward pass할 때 h_t에 대한 loss 미분값을 얻고 loss에 대한 h_t-1의 미분값을 계산한다.
gradient가 tanh gate를 타고 흘러간 다음 'Mat mul gate'를 통과한다. Mat mul gate의 backpropagation은 transpose(가중치 행렬)를 곱하게 된다. 이것은 매번 vanilla RNN cells를 하나 통과할 때마다 가중치 행렬의 일부를 곱하게 된다는 것을 의미한다.

우리가 h_0에 대한 gradient를 구하고자 하면 모든 RNN Cells를 거쳐야 해서 많은 가중치 행렬W가 개입하게 된다.
만약 수백개의 스텝이 있다면 수백번을 곱해주어야 하기 때문에 매우 좋지 않다. 1보다 큰 값을 곱한다면 값이 점점 커지고 1보다 작은 값을 곱한다면 점점 작아져서 0이 될 것이다. 이러한 상황이 발생하지 않는 경우는 곱해지는 값이 1인 경우이다. (하지만 실제로 1이 되는 것는 드물다.)

Largest 특이값(singular value) > 1일 때, 즉 특잇값이엄청 큰 행렬을 계속 곱하는 경우, h_0의 gradient는 아주 커진다.
▶ Exploding gradient problem (backpropagation 시 레이어가 깊어질수록 gradient가 기하급수적으로 증가하는 현상)
Largest 특이값(singular value) < 1일 때, h_0의 gradient는 기하급수적으로 작아진다.
▶ Vanising gradient problem (backpropagation 시 레이어가 깊어질수록 gradient가 기하급수적으로 감소하는 현상)

Exploding gradients일 때, "Graident clipping" 기법을 사용한다.
Gradient clipping이란, gradient를 계산하고 gradient의 L2 norm이 임계값(threshold)보다 큰 경우, gradient가 최대 임계값(threshold)을 넘지 못하도록 조정해준다. 좋은 방법은 아니지만 많은 사람들이 RNN 학습에 이 방법을 사용한다.

Vanishing gradient일 때는 좀 더 복잡한 RNN 아키텍쳐가 필요하다. 바로 LSTM이다.
5. LSTM (Long Short Term Memory)

LSTM은 vanishing & exploding gradients 문제를 완화시키기 위해 디자인되었다. "gradient clipping"과 같은 hack을 쓰지 말고, gradient가 잘 전달되도록 아키텍쳐 자체를 디자인한 경우이다.
vanila RNN은 hidden state가 있어 매 스텝 재귀적인 방법으로 hidden state를 업데이트했다.
반면 LSTM은 한 Cell당 2개의 hidden state가 있다. h_t는 vanila RNN의 hidden state(h_t)와 유사하다. c_t(cell state)는 LSTM 내부에만 존재하며 밖에 노출되지 않는 변수이다.
LSTM은 h_t-1, x_t 2개의 입력을 받는다. 그리고 i, f, o, g 4개의 gates를 계산한다. 이 gates은 c_t를 업데이트 하는데에 사용을 하며 c_t로 다음 스텝의 hidden state를 업데이트한다.

LSTM도 이전 hidden state인 h_t, 현재의 입력인 x_t를 입력으로 받는다.
vanilla RNN의 경우, 두 입력을 concat하고 행렬곱 연산으로 hidden state를 직접 구하였다. 하지만 LSTM은 h_t, x_t를 받아서 쌓아두고 4개의 gates 값을 계산하기 위해 큰 가중치 행렬을 곱해준다. 각 gates 출력은 hidden state의 크기와 동일하다.
gates는 [i, f, o, g] 총 4개가 있다.
* i(input gate) : cell에서의 입력(x_t)에 대한 가중치이다.
* f(forget gate) : 이전 스텝의 cell 정보를 얼마나 망각할 지에 대한 가중치이다.
* o(output gate) : c_t를 얼마나 밖에 드러내 보일지에 대한 가중치이다.
* g(gate gate) : input cell을 얼마나 포함시킬지 결정하는 가중치이다.
각 gate에서 사용하는 비선형함수는 각각 다르다.
i, f, o gate는 sigmoid를 사용한다. gate의 값이 0~1 사이라는 의미이다. 반면 g gate는 tanh를 사용하기에 gate의 값이 -1 ~ 1의 값을 갖는다.

c_t는 현재 스텝에서 사용될 수 있는 '후보'라고 할 수 있다.
2개의 독립적인 scaler 값(f, i)에 의해 조정이 되며 f, i 값은 1까지 증가하거나 감소한다.
f * c_t-1
식을 보면 이전 스텝의 cell state(c_t+1)는 forget gate와 아다마르 곱(element-wise multiplication/같은 크기의 두 행렬의 각 성분을 곱하는 연산)을 한다. 그 결과, 0 또는 1일 것이다. 따라서 forget gate = 0인 element는 이전 cell state를 잊는다. 반면 forget gate = 1이면 cell state의 element를 계속 기억한다.
▶ 이전 스텝의 cell state(c_t-1)를 기억할지 말지 결정 (forget gate에 달림)
i * g
벡터 i는 sigmoid로부터 나온 값으로 0 또는 1이다. cell state의 각 element에 대해서 cell state를 사용하고 싶으면 i = 1, 쓰고 싶지 않으면 i = 0이 된다. gate gate는 tanh 출력이기에 값이 -1 또는 1이다.
▶ 각 스텝마다 1까지 cell state의 각 요소를 증가시키거나 감소시킬 수 있다.

cell state는 counter 개념으로 각 스텝마다 최대 1 또는 -1씩 세는데, 이 값은 tanh를 통과한다. 그리고 최종적으로 output gate와 곱해진다.
output gate는 sigmoid에서 나온 값으로 0 ~ 1의 값을 가진다.


vanilla RNN은 backward pass에서 가중치 행렬W가 계속해서 곱해지는 문제가 있었다. 하지만 LSTM은 다르다.
gradient는 upstream gradient(출력 부에서 backward pass되는gradient)와 forget gate의 곱이다. (cell state의 backpropagation은 upstream gradient * forget gate이다.)
위와 같은 특성이 vanilla RNN에 비해 좋은 점이 있다.
1. forget gate와의 곱셉은 matrix multiplication(행렬 곱셈)이 아니라 element wise multiplication(아다마르 곱셈)이라는 점
2. element wise multiplication(아다마르 곱셈)을 통해 매 스텝 다른 값의 forget gate와 곱해질 수 있다는 점
(vanilla RNN은 동일한 가중치 행렬(h_t)만을 계속 곱하였기에 exploding, vanishing gradient 문제를 일으켰다.)
또한 forget gate는 sigmoid에서 나온 값으로 0~1사이의 값이 된다. 반복적으로 곱하였을 때 좋은 수치적 특성을 보일 수 있다.
3. vanilla RNN의 back ward pass에서 매 스텝 gradient가 tanh를 거쳐야 했다. 하지만 LSTM은 한번만 tanh를 거치면 된다.

LSTM의 Cell state의 아다마르 곱이 gradient를 위한 고속도로 역할을 한다.
6. Other RNN Variants

다양한 RNN 아키텍쳐의 변형된 버전들이 존재한다. 그 중 LSTM 다음으로 유명한 아키텍쳐는 'GRU(Gated Recurrent Unit)'이다. LSTM과 유사하게 생겼다.
7. Summary
* RNN로 다양한 아키텍쳐를 만들 수 있다.
* vanilla RNN은 간단하지만 잘 작동하진 않는다.
* LSTM 또는 GRU를 일반적으로 사용한다.
* RNN는 exploding, vanishing gradient 문제가 있다. exploding은 'gradient clipping'으로 조절이 되며, vanishing은 LSTM와 같은 아키텍쳐로 조절이 가능하다.
* CNN/RNN 아키텍쳐 간에는 교집합이 많다.
참고 자료
'AIFFEL > cs231n' 카테고리의 다른 글
| [풀잎스쿨/cs231n] Lecture 2. Image Classification pipeline (0) | 2022.02.19 |
|---|